Error function
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a function defined as:[1]
| Error function | |
|---|---|
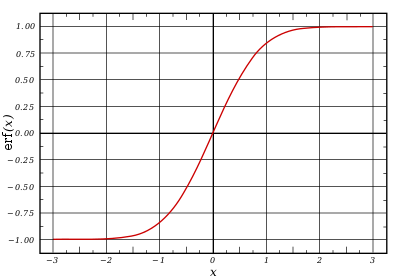 Plot of the error function over real numbers | |
| General information | |
| General definition | |
| Fields of application | Probability, thermodynamics, digital communications |
| Domain, codomain and image | |
| Domain | |
| Image | |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative | |
| Antiderivative | |
| Series definition | |
| Taylor series | |
The integral here is a complex contour integral which is path-independent because is holomorphic on the whole complex plane . In many applications, the function argument is a real number, in which case the function value is also real.
In some old texts,[2] the error function is defined without the factor of . This nonelementary integral is a sigmoid function that occurs often in probability, statistics, and partial differential equations.
In statistics, for non-negative real values of x, the error function has the following interpretation: for a real random variable Y that is normally distributed with mean 0 and standard deviation , erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function is defined as
and the imaginary error function is defined as
where i is the imaginary unit.
Name
[edit]The name "error function" and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with "the theory of Probability, and notably the theory of Errors."[3] The error function complement was also discussed by Glaisher in a separate publication in the same year.[4] For the "law of facility" of errors whose density is given by (the normal distribution), Glaisher calculates the probability of an error lying between p and q as:

Applications
[edit]When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L > μ, it can be shown via integration by substitution:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties
[edit]The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z: where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series
[edit]The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges. For x >> 1, however, cancellation of leading terms makes the Taylor expansion unpractical.
The defining integral cannot be evaluated in closed form in terms of elementary functions (see Liouville's theorem), but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function's Maclaurin series as: which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful: because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is: which holds for every complex number z.
Derivative and integral
[edit]The derivative of the error function follows immediately from its definition: From this, the derivative of the imaginary error function is also immediate: An antiderivative of the error function, obtainable by integration by parts, is An antiderivative of the imaginary error function, also obtainable by integration by parts, is Higher order derivatives are given by where H are the physicists' Hermite polynomials.[5]
Bürmann series
[edit]An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann's theorem:[7] where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions
[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series[8] where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators): (After cancellation the numerator and denominator values in OEIS: A092676 and OEIS: A092677 respectively; without cancellation the numerator terms are values in OEIS: A002067.) The error function's value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[9]
For any real x, Newton's method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges: where ck is defined as above.
Asymptotic expansion
[edit]A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has where the remainder is which follows easily by induction, writing and integrating by parts.
The asymptotic behavior of the remainder term, in Landau notation, is as x → ∞. This can be found by For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion
[edit]A continued fraction expansion of the complementary error function was found by Laplace:[10][11]
Factorial series
[edit]The inverse factorial series: converges for Re(z2) > 0. Here zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[12][13] There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations
[edit]Approximation with elementary functions
[edit]-
Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[14]
-
The above have been generalized to sums of N exponentials[15] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[16] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[17] who showed for the appropriate choice of parameters {A,B} that They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[18]
- A single-term lower bound is[19] where the parameter β can be picked to minimize error on the desired interval of approximation.
-
Another approximation is given by Sergei Winitzki using his "global Padé approximations":[20][21]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[22]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[23] with and
- An approximation of with a maximum relative error less than in absolute value is:[24] for , and for
- A simple approximation for real-valued arguments could be done through Hyperbolic functions: which keeps the absolute difference .
Table of values
[edit]| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
Related functions
[edit]Complementary error function
[edit]The complementary error function, denoted erfc, is defined as

which also defines erfcx, the scaled complementary error function[25] (which can be used instead of erfc to avoid arithmetic underflow[25][26]). Another form of erfc x for x ≥ 0 is known as Craig's formula, after its discoverer:[27] This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[28]
Imaginary error function
[edit]The imaginary error function, denoted erfi, is defined as

where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[25]).
Despite the name "imaginary error function", erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function
[edit]The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,

or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer's function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function, sgn x is the sign function.
Iterated integrals of the complementary error function
[edit]The iterated integrals of the complementary error function are defined by[29]
The general recurrence formula is
They have the power series from which follow the symmetry properties and
Implementations
[edit]As real function of a real argument
[edit]- In POSIX-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[30] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[31]
As complex function of a complex argument
[edit]libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
References
[edit]- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Whittaker, Edmund Taylor; Watson, George Neville (2021). Moll, Victor Hugo (ed.). A Course of Modern Analysis (5th revised ed.). Cambridge University Press. p. 358. ISBN 978-1-316-51893-9.
- ^ Glaisher, James Whitbread Lee (July 1871). "On a class of definite integrals". London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). "On a class of definite integrals. Part II". London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ Weisstein, Eric W. "Erf". MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). "On Bürmann's Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion". The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. "Bürmann's Theorem". MathWorld.
- ^ Dominici, Diego (2006). "Asymptotic analysis of the derivatives of the inverse error function". arXiv:math/0607230.
- ^ Bergsma, Wicher (2006). "On a new correlation coefficient, its orthogonal decomposition and associated tests of independence". arXiv:math/0604627.
- ^ Pierre-Simon Laplace, Traité de mécanique céleste, tome 4 (1805), livre X, page 255.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Schlömilch, Oskar Xavier (1859). "Ueber facultätenreihen". Zeitschrift für Mathematik und Physik (in German). 4: 390–415.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). "New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels" (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). "Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials". IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). "Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]". Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). "An improved approximation for the Gaussian Q-function" (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). "Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function". IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). "Chernoff-Type Bounds for the Gaussian Error Function". IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). "Uniform approximations for transcendental functions". Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). "Global Padé approximations of the generalized Mittag-Leffler function and its inverse". Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). "A handy approximation for the error function and its inverse".
- ^ Press, William H. (1992). Numerical Recipes in Fortran 77: The Art of Scientific Computing. Cambridge University Press. p. 214. ISBN 0-521-43064-X.
- ^ Dia, Yaya D. (2023). "Approximate Incomplete Integrals, Application to Complementary Error Function". SSRN Electronic Journal. doi:10.2139/ssrn.4487559. ISSN 1556-5068.
- ^ a b c Cody, W. J. (March 1993), "Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers" (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), "On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand", Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). "A Novel Extension to Craig's Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis". IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959). Conduction of Heat in Solids (2nd ed.). Oxford University Press. p. 484. ISBN 978-0-19-853368-9.
- ^ "math.h - mathematical declarations". opengroup.org. 2018. Retrieved 21 April 2023.
- ^ "Special Functions – GSL 2.7 documentation".
Further reading
[edit]- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 7". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), "Section 6.2. Incomplete Gamma Function and Error Function", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, archived from the original on 11 August 2011, retrieved 9 August 2011
- Temme, Nico M. (2010), "Error Functions, Dawson's and Fresnel Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.



















![{\displaystyle {\begin{aligned}\Pr[X\leq L]&={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\frac {L-\mu }{{\sqrt {2}}\sigma }}\\&\approx A\exp \left(-B\left({\frac {L-\mu }{\sigma }}\right)^{2}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)
![{\displaystyle \Pr[X\leq L]\leq A\exp(-B\ln {k})={\frac {A}{k^{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)
![{\displaystyle {\begin{aligned}\Pr[L_{a}\leq X\leq L_{b}]&=\int _{L_{a}}^{L_{b}}{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} x\\&={\frac {1}{2}}\left(\operatorname {erf} {\frac {L_{b}-\mu }{{\sqrt {2}}\sigma }}-\operatorname {erf} {\frac {L_{a}-\mu }{{\sqrt {2}}\sigma }}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2214f0db2c1d36075815825b616501175c6283)



![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)\\[6pt]&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{\displaystyle {\begin{aligned}\operatorname {erfi} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z+{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}+{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}+\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)





![{\displaystyle {\begin{aligned}\operatorname {erf} x&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left(1-{\frac {1}{12}}\left(1-e^{-x^{2}}\right)-{\frac {7}{480}}\left(1-e^{-x^{2}}\right)^{2}-{\frac {5}{896}}\left(1-e^{-x^{2}}\right)^{3}-{\frac {787}{276480}}\left(1-e^{-x^{2}}\right)^{4}-\cdots \right)\\[10pt]&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+\sum _{k=1}^{\infty }c_{k}e^{-kx^{2}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164e7f029977edb47c83845b04abfe5b2d28b837)



![{\displaystyle {\begin{aligned}c_{k}&=\sum _{m=0}^{k-1}{\frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}\\[1ex]&=\left\{1,1,{\frac {7}{6}},{\frac {127}{90}},{\frac {4369}{2520}},{\frac {34807}{16200}},\ldots \right\}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60b92e6567d78bdd3d0f9c40f133acd22efba6a4)



![{\displaystyle {\begin{aligned}\operatorname {erfc} x&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left(1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{\left(2x^{2}\right)^{n}}}\right)\\[6pt]&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a11e2e5b22ca898c74f2e913d276c9ac11124a)






![{\displaystyle {\begin{aligned}\operatorname {erfc} z&={\frac {e^{-z^{2}}}{{\sqrt {\pi }}\,z}}\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}Q_{n}}{{\left(z^{2}+1\right)}^{\bar {n}}}}\\[1ex]&={\frac {e^{-z^{2}}}{{\sqrt {\pi }}\,z}}\left[1-{\frac {1}{2}}{\frac {1}{(z^{2}+1)}}+{\frac {1}{4}}{\frac {1}{\left(z^{2}+1\right)\left(z^{2}+2\right)}}-\cdots \right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b359b038af7346ddd06a76b88e1d18da24652fe7)
![{\displaystyle {\begin{aligned}Q_{n}&{\overset {\text{def}}{{}={}}}{\frac {1}{\Gamma {\left({\frac {1}{2}}\right)}}}\int _{0}^{\infty }\tau (\tau -1)\cdots (\tau -n+1)\tau ^{-{\frac {1}{2}}}e^{-\tau }\,d\tau \\[1ex]&=\sum _{k=0}^{n}\left({\frac {1}{2}}\right)^{\bar {k}}s(n,k),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba8dec76e353267c034974169f70531e414aa310)





![{\displaystyle {\begin{aligned}\operatorname {erfc} x&\leq {\frac {1}{2}}e^{-2x^{2}}+{\frac {1}{2}}e^{-x^{2}}\leq e^{-x^{2}},&\quad x&>0\\[1.5ex]\operatorname {erfc} x&\approx {\frac {1}{6}}e^{-x^{2}}+{\frac {1}{2}}e^{-{\frac {4}{3}}x^{2}},&\quad x&>0.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ff659296f7f9a90bd9433d9ea857cde5d4ac1ae)


















![{\displaystyle {\begin{aligned}\operatorname {erfc} x&=1-\operatorname {erf} x\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\\[5pt]&=e^{-x^{2}}\operatorname {erfcx} x,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4acd0062271e2a19c209a02c8cc33d44a28af7cc)


![{\displaystyle {\begin{aligned}\operatorname {erfi} x&=-i\operatorname {erf} ix\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{t^{2}}\,\mathrm {d} t\\[5pt]&={\frac {2}{\sqrt {\pi }}}e^{x^{2}}D(x),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd2dd94cd6d0325224d412f6b5e5ed63ca81d4a)

![{\displaystyle {\begin{aligned}\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t\\[6pt]&={\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x}{\sqrt {2}}}\right)\\[6pt]&={\frac {1}{2}}\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a9e9eaaddcd7a91ade15a41b8d1e272d437559)
![{\displaystyle {\begin{aligned}\operatorname {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\[6pt]\operatorname {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)\\&=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c84a4d2d79631fe9996e30f1d6c0da3089bfe2)




![{\displaystyle {\begin{aligned}i^{n}\!\operatorname {erfc} z&=\int _{z}^{\infty }i^{n-1}\!\operatorname {erfc} \zeta \,\mathrm {d} \zeta \\[6pt]i^{0}\!\operatorname {erfc} z&=\operatorname {erfc} z\\i^{1}\!\operatorname {erfc} z&=\operatorname {ierfc} z={\frac {1}{\sqrt {\pi }}}e^{-z^{2}}-z\operatorname {erfc} z\\i^{2}\!\operatorname {erfc} z&={\tfrac {1}{4}}\left(\operatorname {erfc} z-2z\operatorname {ierfc} z\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/859d2bdbd18db6bb74513716399eebd1b50c88db)



