Affirming a disjunct

The formal fallacy of affirming a disjunct also known as the fallacy of the alternative disjunct or a false exclusionary disjunct occurs when a deductive argument takes the following logical form:^[1]

A or B

A

Therefore, not B

Or in logical operators:

p\vee q

p

{}\vdash {}

¬

q

Where ${}\vdash {}$ denotes a logical assertion.

Explanation

Venn diagram for "A or B", with inclusive or (OR)

Venn diagram for "A or B", with exclusive or (XOR)

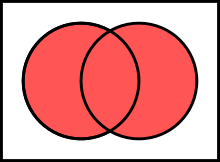
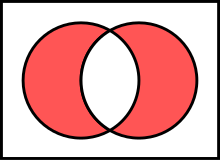
The fallacy lies in concluding that one disjunct must be false because the other disjunct is true; in fact they may both be true because "or" is defined inclusively rather than exclusively. It is a fallacy of equivocation between the operations OR and XOR.

Affirming the disjunct should not be confused with the valid argument known as the disjunctive syllogism.^[2]

Examples

The following argument indicates the unsoundness of affirming a disjunct:

Max is a mammal or Max is a cat.

Max is a mammal.

Therefore, Max is not a cat.

This inference is unsound because all cats, by definition, are mammals.

A second example provides a first proposition that appears realistic and shows how an obviously flawed conclusion still arises under this fallacy.^[3]

To be on the cover of Vogue Magazine, one must be a celebrity or very beautiful.

This month's cover was a celebrity.

Therefore, this celebrity is not very beautiful.

References

^ Sinnott-Armstrong, Walter; Simmons, Claire (2021-12-15). "Some common fallacies in arguments from M/EEG data". NeuroImage. 245: 118725. doi:10.1016/j.neuroimage.2021.118725. ISSN 1095-9572. PMID 34813968.
^ Lay, Steven (2014). Introduction to Analysis with Proof, 5th edition. Pearson. ISBN 978-0321747471.
^ Rosen, Kenneth H. (2019). Discrete Mathematics and its Applications: Kenneth H. Rosen. McGraw-Hill. ISBN 978-1260091991.

External links

Fallacy files: affirming a disjunct
Bennett, Robert "Bo". "Affirming a Disjunct". Logically Fallacious. Retrieved 2023-07-29.

[1] Sinnott-Armstrong, Walter; Simmons, Claire (2021-12-15). "Some common fallacies in arguments from M/EEG data". NeuroImage. 245: 118725. doi:10.1016/j.neuroimage.2021.118725. ISSN 1095-9572. PMID 34813968.

[2] Lay, Steven (2014). Introduction to Analysis with Proof, 5th edition. Pearson. ISBN 978-0321747471.

[3] Rosen, Kenneth H. (2019). Discrete Mathematics and its Applications: Kenneth H. Rosen. McGraw-Hill. ISBN 978-1260091991.

[1]

[2]

[3]

Explanation

Examples

See also

References

External links